DSP (ex: 音響、通訊設備) 的目的都是希望達到無失真的傳遞,在輸出端重現原始訊號,因此,理想的訊號處理系統,在不同頻率範圍,需表現均勻的強度響應。頻率響應 Frequency Response 是用來衡量系統在特定頻率範圍的操作特性。
音響設備可用頻率響應來衡量品質,ex: 理想的喇叭,在人類聽力範圍中 20Hz~20kHz,應該具備等值的頻率響應,藉以達到原音重現。
頻率響應的定義:
系統對於輸入訊號在特定頻率範圍的響應情形,可定義為頻率的函式,響應則包含強度 Magnitude 與相位角 Phase Angle 等等量化數據,通常是以頻譜的方式呈現,用來表示系統的操作特性。
典型的 DSP (LTI) 系統, x[n] 為輸入訊號,經過 h[n] 脈衝響應(impulse response, 也稱為濾波器 filter),得到 y[n] 輸出訊號
如果 DSP 牽涉卷積運算 \(y[n]=h[n]*x[n]\)
根據卷積定理 Covolution Theorem 則
\(F\{y[n]\} = F\{h[n]*x[n]\} = F\{h[n]\} \cdot F\{x[n]\}\)
或是以離散時間傅立葉轉換可表示成:
\(Y(e^{jω}) = H(e^{jω}) \cdot X(e^{jω})\)
因此系統的頻率響應為:
\(H(e^{jω}) = \frac{Y(e^{jω})}{X(e^{jω})}\)
根據 z 轉換,系統的頻率響應跟轉換函式的關係,可表示為:
\(H(e^{jω}) = H(z)|_{z=e^{jω}}\)
因此系統的頻率響應,可表示為
\(H(z) = \frac{Y(z)}{X(z)}\)
其中 X(z), Y(z) 分別為輸入訊號與輸出訊號的 z 轉換結果
DSP 系統的頻率響應 定義為:
\(H(e^{jω}) = \sum_{n=-∞}^{∞} h[n]e^{-jωn}\)
在 LTI 系統,x[n] 是輸入訊號,y[n] 是輸出訊號,卷積運算為:
\(y[n]=\sum_{k=-∞}^{∞}h[k] \cdot x[n-k]\)
假設輸入訊號為複數指數訊號 \(x[n]=e^{jωn}\)
則輸出訊號為 \(y[n]=\sum_{k=-∞}^{∞}h[k] \cdot e^{jω(n-k)} = (\sum_{k=-∞}^{∞}h[k] \cdot e^{jωk})e^{jωn}\)
可改寫為 \(y[n]=H(e^{jω})e^{jωn}\)
因此,可得到以下公式:
\(H(e^{jω}) = \sum_{n=-∞}^{∞}h[n]e^{-jωn}\)
這個公式稱為 DSP 的頻率響應 frequency response
頻率響應就是對脈衝響應 h[n] 求離散時間傅立葉轉換 DTFT 的結果
因為 DTFT 的結果通常是複數,因此經常取其強度 magnitude,與相位角 phase angle
\(|H(e^{jω})|\) 與 \(ang\{H(e^{jω})\}\)
結果都是實數。以圖形表示就是強度頻譜 magnitude spectrum 與相位頻譜 phase spectrum,這是在頻率域的操作特性
頻率響應也常以分貝 decibels, dB 為單位表示,稱為系統的增益 Gain
\(G(ω) = 20 \cdot log_{10}|H(e^{jω}| (dB)\)
濾波器分類
根據系統(濾波器)的頻率響應,可分成以下幾種:
低通濾波器 Lowpass Filter
使得低頻範圍的訊號通過,抑制高頻範圍的訊號,頻率的閥值稱為截止頻率(Cutoff Frequency) ,定義為 \(f_c\),對應的截止角頻率 \(ω_c\)
高通濾波器 Highpass Filter
低通濾波器的相反,讓高頻範圍訊號通過,抑制低頻訊號
帶通濾波器 Bandpass Filter
讓頻率介於 \(f_1 ~ f_2\) 或角頻率 \(ω_1~ω_2\) 之間的訊號通過,抑制其他頻率範圍的訊號
帶阻濾波器 Bandstop Filter
帶通濾波器的相反,抑制頻率範圍落在 \(f_1 ~ f_2\) 或角頻率 \(ω_1~ω_2\) 之間的訊號,使得其他頻率範圍的訊號通過
陷波濾波器 Notch Filter
是帶阻濾波器的一種,僅抑制某個特定頻率,ex: 60Hz 的干擾雜訊。陷波濾波器主要是使得某特定頻率的訊號變為 0,因此也稱為歸零濾波器 Nulling Filter
梳狀濾波器 Comb Filter
Comb Filter 其頻率響應的形狀跟梳子一樣,主要是同時抑制多個頻率範圍,頻率與頻率之間,通常是設定為整數倍數
全通濾波器 All-Pass Filter
讓所有頻率範圍都通過,通常會調整訊號在某些頻率範圍的相位移
濾波器也可根據訊號的型態分成 類比濾波器 Analog Filter,與數位濾波器 Digital Filter
頻率響應範例
介紹幾種經典的頻率響應
理想濾波器
濾波器的用途是讓某些特定範圍的頻率分量通過,抑制其他範圍的頻率分量,為了不造成訊號失真,頻率通過的頻率分量的頻率響應值是設定為 1,抑制的頻率分量,頻率響應值設定為 0。
使得頻率分量通過的頻率範圍稱為通過頻帶 (Passband),抑制的頻率範圍稱為截止頻帶 (Stopband)
理想低通濾波器 Ideal Lowpass Filter
轉換函式:\( H_{LP}(e^{jω}) = \left\{ \begin{array}{ll} 1 & \mbox{if 0 ≤ ω ≤ \)ω_c\(} \\ 0 & \mbox{otherwise} \end{array} \right.\)
在此只定義單邊 Single-Sided 的頻率響應,ω 介於 0 ~ π 之間,且 \(ω_c=2 \pi f_c\),其中 \(f_c\) 稱為截止頻率 Cutoff Frequency
理想高通濾波器 Ideal Highpass Filter
轉換函式:\( H_{HP}(e^{jω}) = \left\{ \begin{array}{ll} 1 & \mbox{if \)ω_c\( < ω ≤ π} \\ 0 & \mbox{otherwise} \end{array} \right.\)
低通與高通濾波器的關係為: \(H_{HP}(e^{jω})=1- H_{LP}(e^{jω})\)
理想帶通濾波器 Ideal Bandpass Filter
轉換函式:\( H_{BP}(e^{jω}) = \left\{ \begin{array}{ll} 1 & \mbox{if \)ω1\( ≤ ω ≤ \)ω2\(} \\ 0 & \mbox{otherwise} \end{array} \right.\)
允許頻率範圍 \(ω_1 ≤ ω ≤ ω_2\) 或頻率 \(f_1 ≤ f ≤ f_2\) 的訊號通過,\(f_1, f_2\) 稱為截止頻率
理想帶阻濾波器 Ideal Bandstop Filter
轉換函式:\( H_{BS}(e^{jω}) = \left\{ \begin{array}{ll} 1 & \mbox{if ω < \)ω1\( or ω > \)ω2\(} \\ 0 & \mbox{otherwise} \end{array} \right.\)
帶通與帶阻濾波器的關係為: \(H_{BS}(e^{jω})=1- H_{BP}(e^{jω})\)
ex: Ideal Lowpass Filter定義如下,求其在離散時間域的脈衝響應 Impulse Response
\( H_{LP}(e^{jω}) = \left\{ \begin{array}{ll} 1 & \mbox{if 0 ≤ ω ≤ \)ω_c\(} \\ 0 & \mbox{otherwise} \end{array} \right.\)
根據 Inverse DTFT 公式
\(x[n] = \frac{1}{2π} \int_{-∞}^{∞}X(e^{jωn})e^{jωn}dω\)
Ideal Lowpass Filter 在離散時間域的脈衝響應為:
\(h_{LP}[n] = \frac{1}{2π} \int_{-∞}^{∞}H_{LP}(e^{jωn})e^{jωn}dω \\ = \frac{1}{2π} \int_{-ω_c}^{ω_c}e^{jωn}dω \\ = \frac{1}{2π} [\frac{1}{jn}e^{jωn}]_{-ω_c}^{ω_c} \\ = \frac{1}{2π} [\frac{e^{jω_cn}}{jn}- \frac{e^{-jω_cn}}{jn} ] \\ = \frac{sin(ω_cn)}{πn} \quad\quad \mbox{-∞<n<∞}\)
當 n=0,使用羅必達規則 L'Hopital's Rule
\(h_{LP}[0] = \lim_{n→0} \frac{sin(ω_cn)}{πn} \\ = \lim_{n→0} \frac{ \frac{d}{dn} sin(ω_cn)}{ \frac{d}{dn} (πn) } \\ = \lim_{n→0} \frac{ cos(ω_cn) \cdot ω_c}{ π } \\ = \frac{ ω_c }{ π }\)
因為 \(-∞ < n < ∞\),無法在離散時間域中,定義有限長度的脈衝響應,藉以實現頻率域中的 ideal lowpass filter。脈衝響應在計算時有用到過去、現在、未來的數位訊號,不是因果系統。脈衝響應不符合絕對可加總 Absolutely Summable 原則,系統也不具 BIBO 穩定性。
用 python 處理離散時間域的脈衝響應時,因為離散序列是有限長度,以近似方式接近 ideal lowpass filter。原則上採用的濾波器大小,是使用奇數
當 filter 大小為 5時,-2<n<2
當 filter 大小為 11 時,-5<n<5
ideal lowpass filter 的脈衝響應,具有 sinc 函數的特性,向左右兩邊無限延伸
以下範例選擇 \(ω_c=\frac{\pi}{2}\),因此當 n=0,\(\frac{ω_c}{\pi}=0.5\) ,可調整 \(ω_c\) 觀察脈衝響應的結果
import numpy as np
import matplotlib.pyplot as plt
def plot(filter_size, plotpos):
filter_half = int( filter_size / 2 )
wc = np.pi / 2
na = np.arange( -filter_half, filter_half + 1 ) # 定義 n 陣列
h = np.zeros( filter_size ) # 計算脈衝響應
for n in na:
if n == 0:
h[n+filter_half] = wc/np.pi
else:
h[n+filter_half] = np.sin( wc * n ) / ( np.pi * n )
plt.subplot(plotpos)
plt.stem( na, h, use_line_collection=True )
plt.xlabel( 'n (filter_size='+ str(filter_size) +')')
plt.ylabel( 'h[n]' )
plot(5, 221)
plot(11, 222)
plot(21, 223)
plot(31, 224)
plt.show( )
以下選擇 \(ω_c=\frac{\pi}{10}\),因此當 n=0,\(\frac{ω_c}{\pi}=1/10\)
由於有限長度的脈衝響應,無法提供 ideal filter 的操作特性,在 DSP 實際應用時,通常是讓頻率響應在通過頻帶與截止頻帶之間,由 1 逐漸降為 0,且在通過頻帶或截止頻帶內,頻率響應允許有些微變動。
剛剛是求濾波器大小 5, 11,21, 31 的脈衝響應,現在改求頻率響應。
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
def plot(filter_size, plotpos):
filter_half = int( filter_size / 2 )
wc = np.pi / 2
na = np.arange( -filter_half, filter_half + 1 ) # 定義 n 陣列
h = np.zeros( filter_size ) # 計算脈衝響應
for n in na:
if n == 0:
h[n+filter_half] = wc/np.pi
else:
h[n+filter_half] = np.sin( wc * n ) / ( np.pi * n )
w, H = signal.freqz( h )
mag = abs( H )
plt.subplot(plotpos)
plt.plot( w, mag )
plt.xlabel( r'$\omega$'+' (filter_size='+ str(filter_size) +')' )
plt.ylabel( 'Magnitude' )
plot(5, 221)
plot(11, 222)
plot(21, 223)
plot(31, 224)
plt.show( )結果發現,若 filter size 越大,或脈衝響應樣本越多,越接近理想的 lowpass filter。此外可注意到頻率響應在通過頻帶與截止頻帶之間,出現了 Gibbs 現象。
平均濾波器
average filter 定義為
\(h[n] = \frac{1}{M}{1,1,1,...,1}, n=0,1,...,M-1\) ,M為濾波器大小 filter size
平均濾波器的頻率響應,可根據其 DTFT 得來
\(H(e^{jω}) = \sum_{n=-∞}^{∞}h[n]e^{-jωn} \\ = \frac{1}{M} \sum_{n=0}^{M-1}e^{-jωn} \\ = \frac{1}{M} ( \sum_{n=0}^{∞}e^{-jωn} - \sum_{n=M}^{∞}e^{-jωn}) \\ = \frac{1}{M} ( \sum_{n=0}^{∞}e^{-jωn} ) (1 - e^{-jωM}) \\ = \frac{1}{M} \frac{1 - e^{-jωM}}{1 - e^{-jω}} \\ = \frac{1}{M} \frac{sin(Mω/2)}{sin(ω/2)} e^{-j(M-1)ω/2} \)
取其強度 magnitude
\(|H(e^{jω})| = |\frac{sin(Mω/2)}{sin(ω/2)}|\)
以圖形表示,就是平均濾波器的頻率響應
ex: 若平均濾波器定義 \(h[n]=\frac{1}{M}{1,1,...,1}, n=0,1,...,M-1\)
當 M=5, 15,求其頻率響應
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
def average_filter(filter_size):
h = np.ones( filter_size ) / filter_size
return h
def plot(filter_size, plotpos):
h = average_filter(filter_size)
w, H = signal.freqz( h )
mag = abs( H )
plt.subplot(plotpos)
plt.plot( w, mag )
plt.xlabel( r'$\omega$'+' (filter_size='+ str(filter_size) +')' )
plt.ylabel( 'Magnitude' )
plot(5, 121)
plot(15, 122)
plt.show( )平均濾波器有 lowpass filter 的特性,當 size 越小,通過頻帶越寬。但平均濾波器有允許少量高頻分量通過
高斯濾波器
Gaussian Filter 可定義為
\(g[n]=e^{-n^2/2σ^2}\) ,其中 σ 為標準差
chap9: 高斯函數的傅立葉轉換,形成另一個高斯函數。因此高斯函數的頻率響應,可用另一個高斯函數表示
ex: Gaussian Filter 定義為 \(g[n]=e^{-n^2/2σ^2}\) ,當 σ=1, 3,求其頻率響應
note: 程式中有對係數進行正規化,讓 \(\sum_{n}g[n]=1\)
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
def plot(sigma, plotpos):
filter_size = int( 6 * sigma + 1 ) # 濾波器大小
gauss = signal.gaussian( filter_size, sigma ) # 濾波器係數
sum = np.sum( gauss ) # 正規化
gauss = gauss / sum
w, H = signal.freqz( gauss )
mag = abs( H )
plt.subplot(plotpos)
plt.plot( w, mag )
plt.xlabel( r'$\omega$'+' (sigma='+ str(sigma) +')' )
plt.ylabel( 'Magnitude' )
plot(sigma=1, plotpos=121)
plot(sigma=3, plotpos=122)
plt.show( )高斯濾波器有 lowpass filter 的特性,標準差越小,通過頻帶較寬。在高頻範圍的抑制效果,比平均濾波器好。
FIR 濾波器
一階 FIR 濾波器有 lowpass, highpass filter 兩種
FIR filters 裡面最簡單的是移動平均濾波器 Moving Averge Filter,濾波器大小為 2
最簡單的 FIR Lowpass Filter 的一階轉換函式定義為:
\(H_0(z)=\frac{1}{2}(1+z^{-1})\)
最簡單的 FIR Highpass Filter 的一階轉換函式定義為:
\(H_1(z)=\frac{1}{2}(1-z^{-1})\)
因為 \(H_1(z) = 1 - H_0(z) = 1-\frac{1}{2}(1+z^{-1}) = \frac{1}{2}(1-z^{-1})\)
ex: 分別求上面兩個 FIR filters 的頻率響應
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
b = np.array( [ 0.5, 0.5 ] ) # 低通濾波器
w, H0 = signal.freqz( b )
H0 = abs( H0 )
b = np.array( [ 0.5, -0.5 ] ) # 高通濾波器
w, H1 = signal.freqz( b )
H1 = abs( H1 )
plt.subplot(121)
plt.plot( w, H0 )
plt.xlabel( r'$\omega$' +' (lowpass)' )
plt.ylabel( 'Magnitude' )
plt.subplot(122)
plt.plot( w, H1 )
plt.xlabel( r'$\omega$' +' (highpass)' )
plt.ylabel( 'Magnitude' )
plt.show( )
根據 Lowpass Filter 的頻率響應,強度的最大/最小值分別是 1 與 0。頻率響應也是從 1 逐漸降到 0。
在討論 Lowpass Filter 時,當截止頻率 \(ω=ω_0\),強度降為
\(|H_0(e^{jω_c})| = \frac{1}{\sqrt{2}}|H_0(e^{j0})|\)
如果以分貝表示則為
\(20 log_{10}|H_0(e^{jω_c})| = 20 log_{10}( \frac{1}{\sqrt{2}}|H_0(e^{j0})| ) \\ = 20 log_{10}|H_0(e^{j0})| - 20 log_{10}\sqrt{2} \\ = 0 - 3.0103 ≈ -3dB\)
\(ω_c\)或 \(f_c\) 稱為 3dB 截止頻率 (3dB Cutoff Frequency),通常被視為是通過頻帶 (Passband) 的邊緣。因此,\(ω_c\)或 \(f_c\) 也常被稱為 通過頻帶邊緣頻率(Passband Edge Frequency)
串接多個 FIR Filter,可用來近似 ideal lowpass filter
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
# order = eval( input( "Enter number of cascade FIR filters: " ) )
def plot(order, plotpos):
b = np.array( [ 0.5, 0.5 ] )
w, H = signal.freqz( b )
for i in range( order - 1 ):
H *= H
H0 = abs( H )
plt.subplot(plotpos)
plt.plot( w, H0 )
plt.xlabel( r'$\omega$' +'(order='+str(order)+')' )
plt.ylabel( 'Magnitude' )
plot(1, 221)
plot(2, 222)
plot(3, 223)
plot(4, 224)
plt.show( )
IIR 濾波器
IIR Lowpass Filter
一階 IIR Lowpass Filter 轉換函式定義為 \(H_0(z)= \frac{1-α}{2} \frac{1+z^{-1}}{1-αz^{-1}}\) ,其中 \(|α|<1\) 為穩定的 IIR Filter
IIR Highpass Filter
一階 IIR Highpass Filter 轉換函式定義為 \(H_1(z)= \frac{1+α}{2} \frac{1-z^{-1}}{1-αz^{-1}}\) ,其中 \(|α|<1\) 為穩定的 IIR Filter
ex: 一階 IIR Lowpass/Highpass Filter,當 α = 0.2, 0.4, 0.6, 0.8 時,求其頻率響應
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
# alpha = eval( input( "Please enter alpha (< 1): " ) )
def iir_lowpass(alpha, plotpos):
b = np.array( [ 1 - alpha, 1 - alpha ] )
a = np.array( [ 2, -2 * alpha ] )
w, H = signal.freqz( b, a )
H0 = abs( H )
plt.subplot(plotpos)
plt.plot( w, H0 )
plt.xlabel( r'$\omega$' +' (alpha='+str(alpha)+')' )
plt.ylabel( 'Magnitude' )
def iir_highpass(alpha, plotpos):
b = np.array( [ 1 + alpha, - ( 1 + alpha ) ] )
a = np.array( [ 2, -2 * alpha ] )
w, H = signal.freqz( b, a )
H1 = abs( H )
plt.subplot(plotpos)
plt.plot( w, H1 )
plt.xlabel( r'$\omega$' +' (alpha='+str(alpha)+')' )
plt.ylabel( 'Magnitude' )
plt.figure( 1 )
iir_lowpass(0.2, 221)
iir_lowpass(0.4, 222)
iir_lowpass(0.6, 223)
iir_lowpass(0.8, 224)
plt.figure( 2 )
iir_highpass(0.2, 221)
iir_highpass(0.4, 222)
iir_highpass(0.6, 223)
iir_highpass(0.8, 224)
plt.show( )IIR Lowpass Filters
IIR Highpass Filters
IIR 帶通濾波器
二階 IIR Bandpass Filter 的轉換函式定義為
\(H_{BP}(z) = \frac{1-α}{2} \frac{1-z^{-2}}{1-β(1+α)z^{-1}+αz^{-2}}\) ,其中 α, β 都小於 1
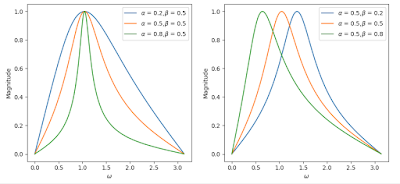
ex1: 當 α = 0.2, 0.5, 0.8 且 β=0.5 時,求其頻率響應
ex2: 當 α = 0.5 且 β=0.2, 0.5, 0.8 時,求其頻率響應
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
def IIR_bandpass_frequency_response(alpha, beta, plotpos):
b = np.array( [ 1 - alpha, 0, -( 1 - alpha ) ] )
a = np.array( [ 2, -2 * beta * ( 1 + alpha ), 2 * alpha ] )
w, H = signal.freqz( b, a )
H1 = abs( H )
plt.subplot(plotpos)
plt.plot( w, H1, '-', label = r'$\alpha$ = '+str(alpha)+','+r'$\beta$ = '+str(beta) )
plt.legend( loc = 'upper right' )
plt.xlabel( r'$\omega$' )
plt.ylabel( 'Magnitude' )
IIR_bandpass_frequency_response(0.2, 0.5, 121)
IIR_bandpass_frequency_response(0.5, 0.5, 121)
IIR_bandpass_frequency_response(0.8, 0.5, 121)
IIR_bandpass_frequency_response(0.5, 0.2, 122)
IIR_bandpass_frequency_response(0.5, 0.5, 122)
IIR_bandpass_frequency_response(0.5, 0.8, 122)
plt.show( )α 參數用來調整頻寬,β 參數用來調整頻率中心
梳狀濾波器
Comb Lowpass Filter
簡易梳狀低通濾波器的轉換函式,可定義為
\(H_{CLP}(z) = \frac{1}{2}(1+z^{-M})\),M 為正整數
Comb Highpass Filter
簡易梳狀高通濾波器的轉換函式,可定義為
\(H_{CHP}(z) = \frac{1}{2}(1-z^{-M})\) ,M 為正整數
ex: 當 M=10,求頻率響應
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
# M = eval( input( "Please enter M for the Comb Filter: " ) )
def comb_lowpass_filter_frequency_response(M, plotpos):
b = np.zeros( M + 1 ) # 梳狀低通濾波器
b[0] = 0.5
b[M] = 0.5
w, H = signal.freqz( b, 1 )
H0 = abs( H )
plt.subplot(plotpos)
plt.plot( w, H0 )
plt.xlabel( r'$\omega$'+' (comb lowpass)' )
plt.ylabel( 'Magnitude' )
def comb_highpass_filter_frequency_response(M, plotpos):
b = np.zeros( M + 1 )
b[0] = 0.5
b[M] = -0.5 # 梳狀高通濾波器
w, H = signal.freqz( b, 1 )
H1 = abs( H )
plt.subplot(plotpos)
plt.plot( w, H1 )
plt.xlabel( r'$\omega$'+' (comb highpass)' )
plt.ylabel( 'Magnitude' )
M = 10
comb_lowpass_filter_frequency_response(M, 121)
comb_highpass_filter_frequency_response(M, 122)
plt.show( )